终于有时间了，前几日正式开始了我的机器学习之旅，总结下目前已掌握的知识。

#机器学习

机器学习本质是一项监督分类/回归问题，"监督"表示你有许多样本，假设你知道这些样本的正确答案，我们不断地把样本交给机器，并告诉机器这些样本是正确或错误的，对机器进行训练，最终达到机器学习的目的。

#监督学习

简单说：监督学习就是教会计算机去完成任务，如：根据你已经标记为垃圾邮件的邮件学习识别垃圾邮件，根据你喜欢的电影推荐其他你可能喜欢的电影...

监督学习可以理解为以下两种模型：

• 回归模型 即：根据之前的数据预测出一个准确的输出值

回归问题通常是用来预测一个值，如预测房价、未来的天气情况等等，例如一个产品的实际价格为500元，通过回归分析预测值为499元，我们认为这是一个比较好的回归分析。 一个比较常见的回归算法是线性回归算法（LR）。另外，回归分析用在神经网络上，其最上层是不需要加上softmax函数的，而是直接对前一层累加即可。回归是对真实值的一种逼近预测。

• 分类模型 即：根据之前的数据和分类/标签将输入数据准确地进行分类

分类问题是用于将事物打上一个标签，通常结果为离散值。例如判断一幅图片上的动物是一只猫还是一只狗，分类通常是建立在回归之上，分类的最后一层通常要使用softmax函数进行判断其所属类别。 分类并没有逼近的概念，最终正确结果只有一个，错误的就是错误的，不会有相近的概念。最常见的分类方法是逻辑回归，或者叫逻辑分类。

分类模型和回归模型本质一样，分类模型可将回归模型的输出离散化，回归模型也可将分类模型的输出连续化。

两者的区别在于输出变量的类型。

• 定量输出称为回归，或者说是连续变量预测；
• 定性输出称为分类，或者说是离散变量预测。

举个例子：

• 预测明天的气温是多少度，这是一个回归任务；
• 预测明天是阴、晴还是雨，就是一个分类任务。

#无监督学习

无监督学习中，我们将让计算机自己进行学习。

无监督学习（也有人叫非监督学习，反正都差不多）是另一种研究的比较多的学习方法，它与监督学习的不同之处，在于我们事先没有任何训练样本，而需要直接对数据进行建模。 这听起来似乎有点不可思议，但是在我们自身认识世界的过程中很多处都用到了无监督学习。

比如我们去参观一个画展，我们完全对艺术一无所知，但是欣赏完多幅作品之后，我们也能把它们分成不同的派别（比如哪些更朦胧一点，哪些更写实一些，即使我们不知道什么叫做朦胧派，什么叫做写实派，但是至少我们能把他们分为两个类）。

无监督学习里典型的例子就是聚类了。聚类的目的在于把相似的东西聚在一起，而我们并不关心这一类是什么。因此，一个聚类算法通常只需要知道如何计算相似度就可以开始工作了。

更多关于无监督学习将在今后的进阶文章中整理。

#两者的区别

机器的整个学习的过程非常像人类的学习习惯，人类通过观察很多示例来进行学习，计算机进行机器学习也是如此，你给他提供很多示例，计算机分析发生了什么并学习，而这个分析学习的过程便是机器学习要解决的核心问题。

下小节摘自 知乎 - 什么是无监督学习？ - 王丰的回答 ：

是否有监督（supervised），就看输入数据是否有标签（label）。输入数据有标签，则为有监督学习，没标签则为无监督学习。

首先看什么是学习（learning）？

一个成语就可概括：举一反三。此处以高考为例，高考的题目在上考场前我们未必做过，但在高中三年我们做过很多很多题目，懂解题方法，因此考场上面对陌生问题也可以算出答案。

机器学习的思路也类似：我们能不能利用一些训练数据（已经做过的题），使机器能够利用它们（解题方法）分析未知数据（高考的题目）？

最简单也最普遍的一类机器学习算法就是分类（classification）。对于分类，输入的训练数据有特征（feature），有标签（label）。所谓的学习，其本质就是找到特征和标签间的关系（mapping）。 这样当有特征而无标签的未知数据输入时，我们就可以通过已有的关系得到未知数据标签。在上述的分类过程中，如果所有训练数据都有标签，则为有监督学习（supervised learning）。

如果数据没有标签，显然就是无监督学习（unsupervised learning）了，也即聚类（clustering）。 目前分类算法的效果还是不错的，但相对来讲，聚类算法就有些惨不忍睹了。确实，无监督学习本身的特点使其难以得到如分类一样近乎完美的结果。 这也正如我们在高中做题，答案（标签）是非常重要的，假设两个完全相同的人进入高中，一个正常学习，另一人做的所有题目都没有答案，那么想必第一个人高考会发挥更好，第二个人会发疯。 这时各位可能要问，既然分类如此之好，聚类如此之不靠谱，那为何我们还可以容忍聚类的存在？ 因为在实际应用中，标签的获取常常需要极大的人工工作量，有时甚至非常困难。 例如在自然语言处理（NLP）中，Penn Chinese Treebank在2年里只完成了4000句话的标签……

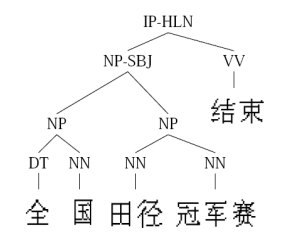
这时有人可能会想，难道有监督学习和无监督学习就是非黑即白的关系吗？有没有灰呢？Good idea。

灰是存在的。二者的中间带就是半监督学习（semi-supervised learning）。对于半监督学习，其训练数据的一部分是有标签的，另一部分没有标签，而没标签数据的数量常常极大于有标签数据数量（这也是符合现实情况的）。 隐藏在半监督学习下的基本规律在于：数据的分布必然不是完全随机的，通过一些有标签数据的局部特征，以及更多没标签数据的整体分布，就可以得到可以接受甚至是非常好的分类结果。 （此处大量忽略细节）因此，learning家族的整体构造是这样的：

• 有监督学习（分类，回归）
• 半监督学习（分类，回归），transductive learning（分类，回归）
• 半监督聚类（有标签数据的标签不是确定的，类似于：肯定不是xxx，很可能是yyy）
• 无监督学习（聚类）

#特征和标签

#提取特征

看下面一张图：

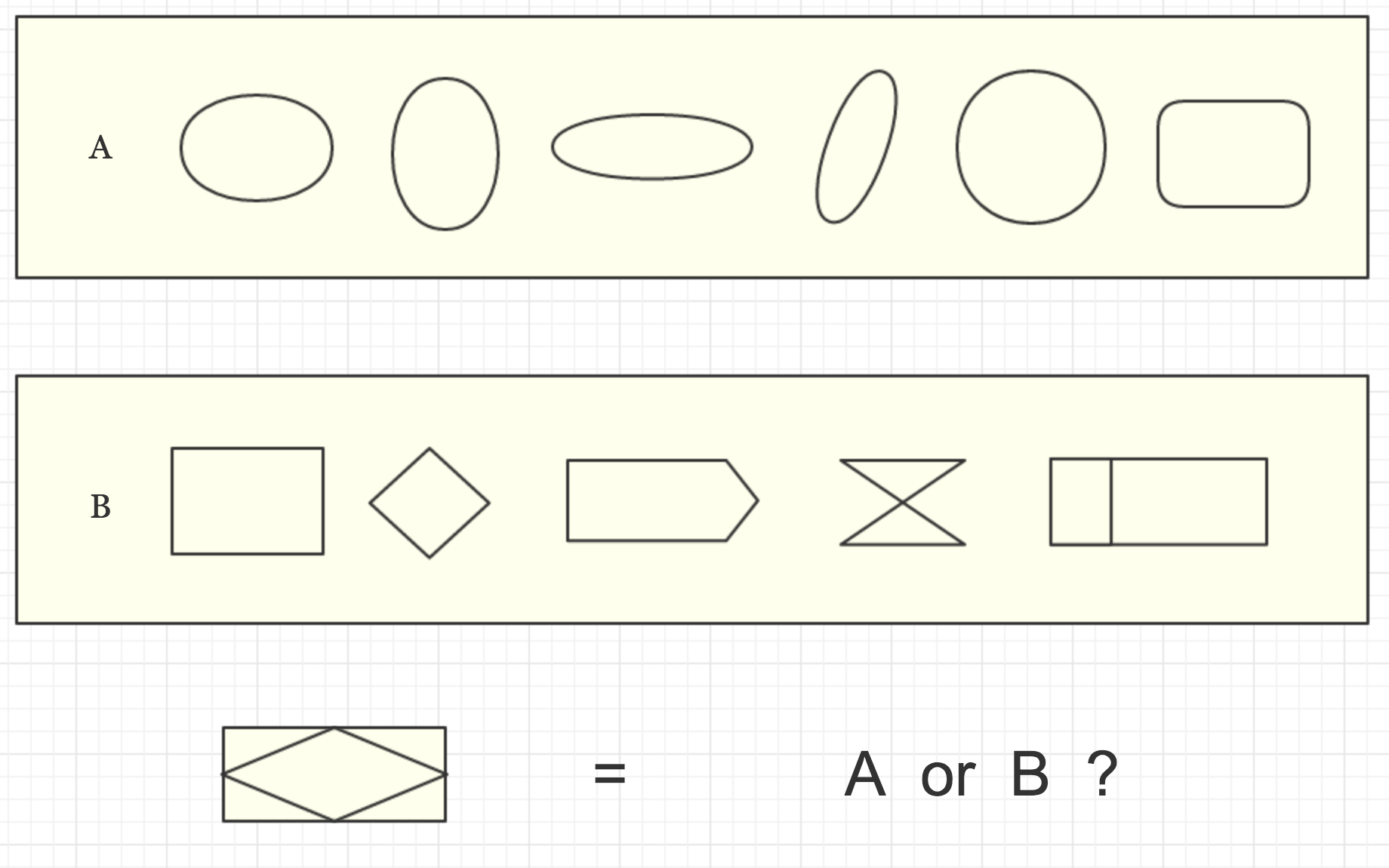
已知A集合中的所有元素和B集合中的所有元素，你认为上图最终元素应该属于A集合还是B集合？

答案是B集合。也许图中的实例数量不足以你进行准确判断（当然这个例子太容易判断啦），如果每个集合扩展到100个元素呢？

很显然，集合中元素的数量越多，我们能够发现出更多的特征，进而做出更准确的判断。

我们之所以能一眼将元素进行判定其属于B集合，是因为我们可以最快识别出元素的特征：角。

当我们大脑对元素的特征进行分析和判断后，大脑最终会一定会反馈出其中一个结果：

• 属于A集合
• 属于B集合
• 属于C集合（如果有的话...）
• ...

最终我们发现B集合的条件满足元素的特征，于是最终确认元素属于B集合。

在机器学习中，我们通常会把特征作为输入，然后尝试生成标签，最终进行分类。

#散点图

在上文中，我们将图形的角数作为特征，然而在实际的问题中，我们可能需要提取完全不一样的特征。

如：如果我们需要实现一个音乐的智能推荐算法，我们首先需要根据用户已经喜欢的音乐中提取特征，这些特征可能是音乐对应的流派、声音性别、节奏强度、平均分贝值...

分析出特征后我们先尝试将特征数据可视化，接下来，我们使用一个散点图来表示上面音乐推荐的例子：

现在，假设Surmon😆喜欢一首音乐叫《天马座的幻想》，我们现在提取出这首音乐的一些特征，包括：强度、歌曲节奏、声音性别、歌曲流派...， 为了简化问题，我们图中在仅使用强度和节奏特征，如图：

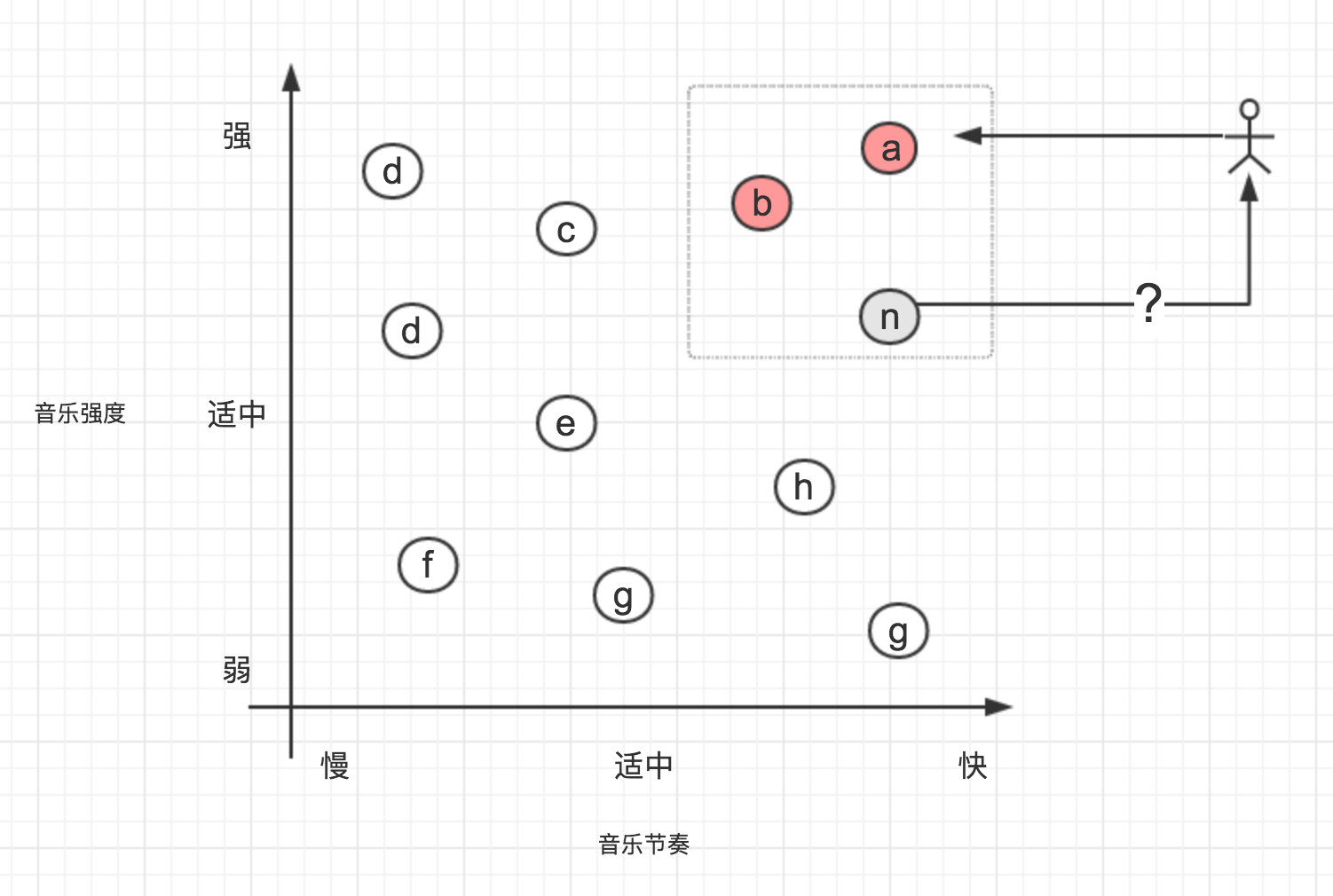
《天马座的幻想》这首音乐，节奏快，强度较高，我们在图中用a点表示； 同样的，我们可以提取其他音乐的这些特征，因此，每首音乐都变成了图中的一个数据点，图中的b、c、d...分别代表其他歌曲；

假设a、b两首音乐为Surmon喜欢的音乐（红色背景标注的），且Surmon不喜欢其他之外的音乐，你认为Surmon会喜欢推荐的音乐n吗？

答案是会喜欢，虽然无法完全确定，起码从图上来判断是的。

又有假设了：

假设Surmon失恋了，又开始喜欢一些节奏比较温柔的轻音乐，于是现在Surmon现在喜欢的音乐数据是这样的，整体看来比较分散：

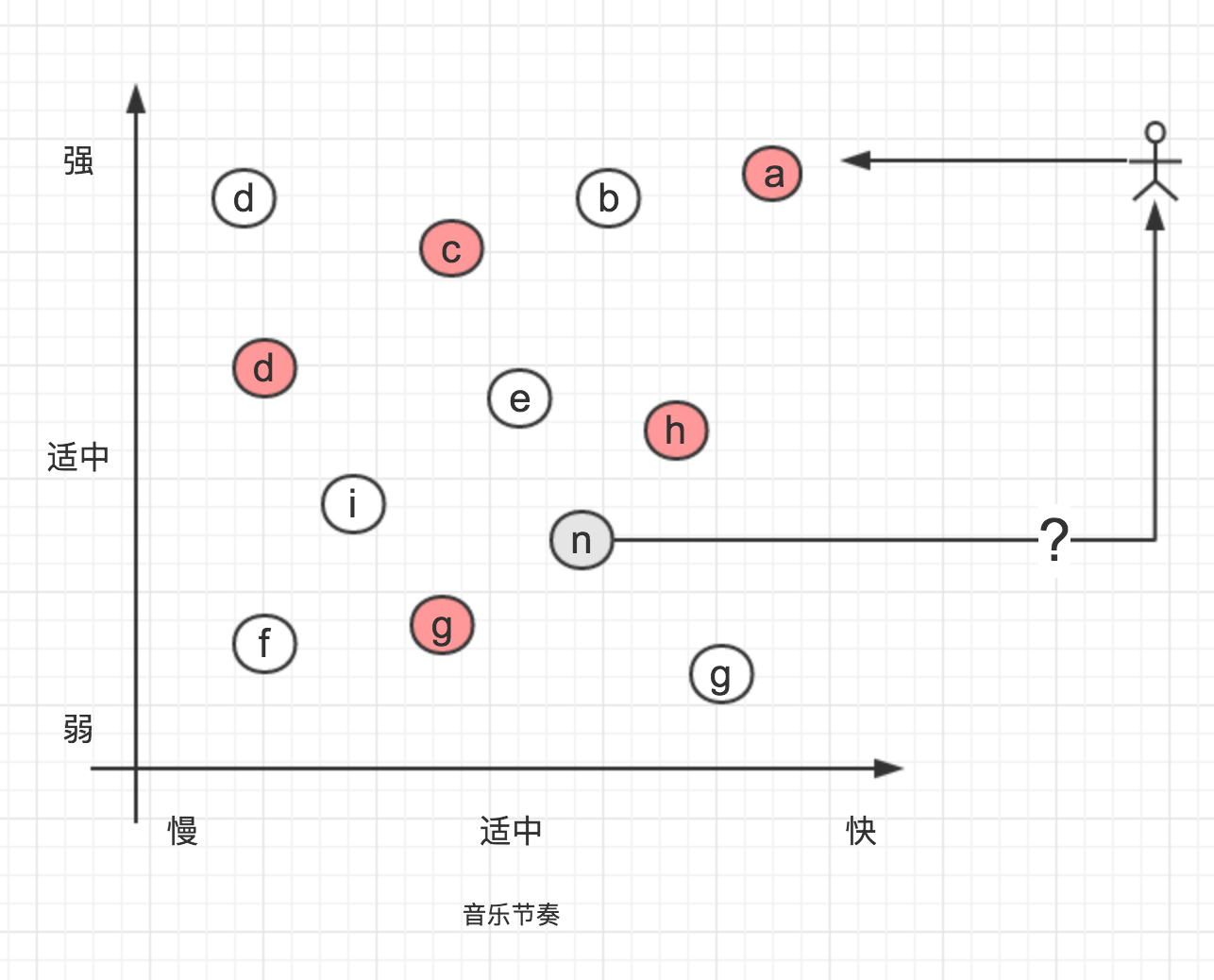
你认为Surmon会喜欢推荐的音乐n吗？

答案是不确定。

但实际上，应该存在一个模式，计算出Surmon喜欢的音乐的数据集，如下，推荐的音乐n可能被包含在Surmon喜欢的音乐的数据集中：

也有可能这首音乐不被包含在Surmon喜欢的音乐的数据集中：

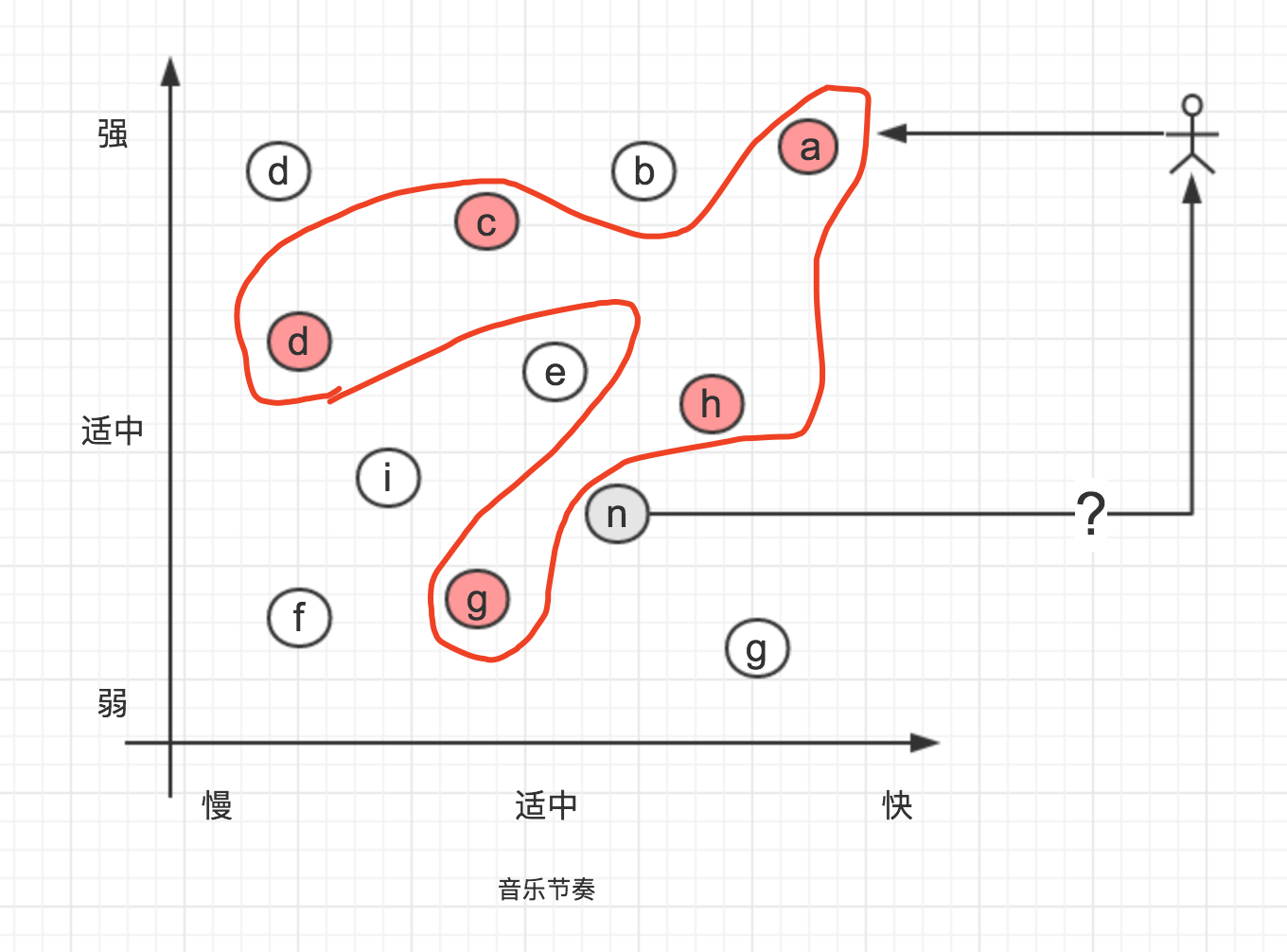
通过观察Surmon喜欢的音乐的数据集，我们便能得出相对准确的结果，即Surmon是否会喜欢这首音乐。

再来一个比较现实的例子：

假设我们在研究汽车的无人驾驶技术，我们需要机器判断出汽车当前面临的环境并作出对应的操作； 假设我们将汽车行驶的环境特征分为：路面平整度(1-3)、行驶坡度(3-6)两个维度，如下图；我们在散点图中以轴线呈现出来，同时将轴线简单分别分为三个维度，对应我们的特征，最终我们会得到9个点：

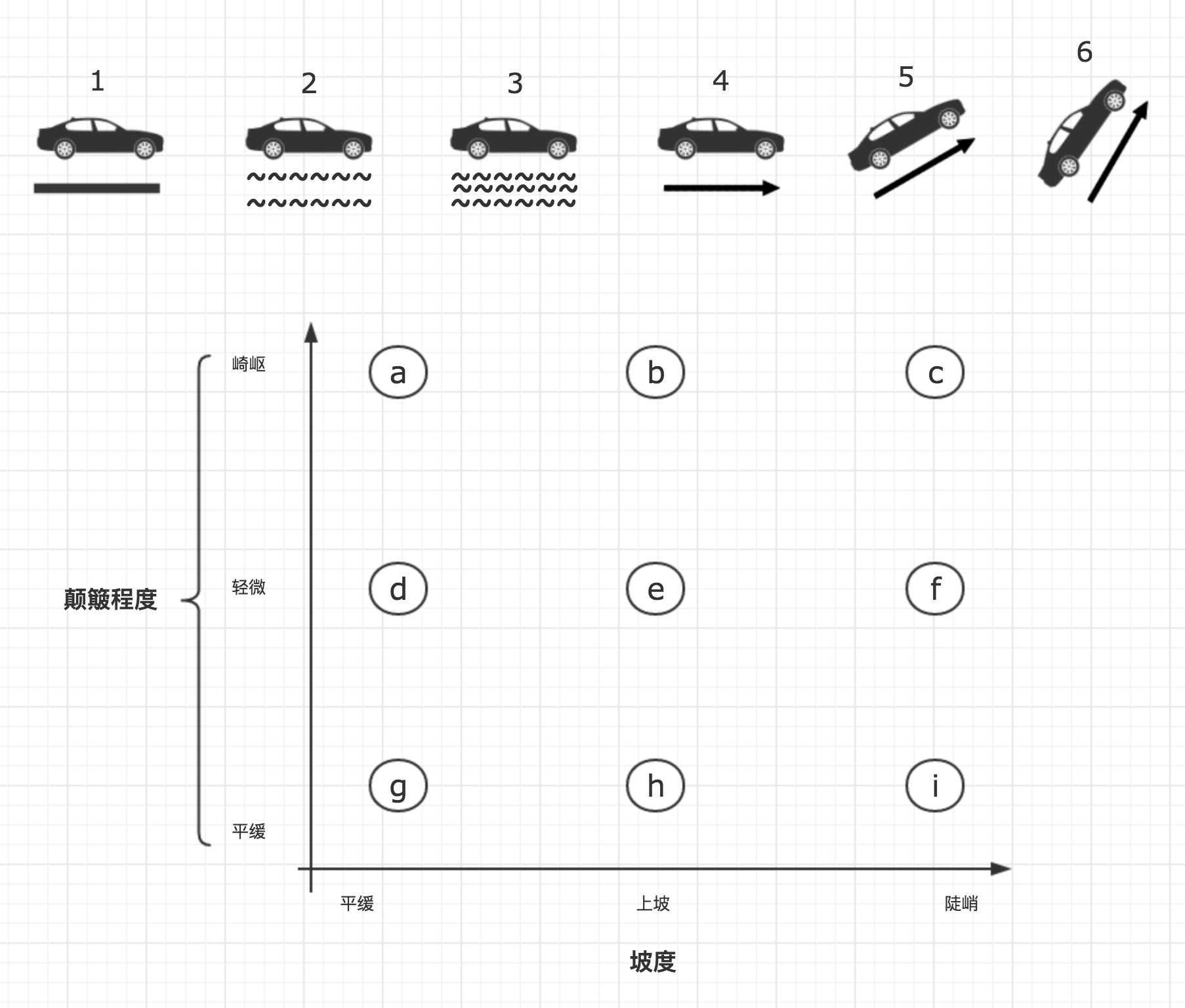
当前，事实上，这两个特征是可能同时发生的，故这9个点代表汽车可能遇到的崎岖程度和坡度所组成的所有特征组合，我们暂且称之为分类。

上图中，汽车在轻微上坡但路面较为平坦时（5号路况），对应h类。

Python scikit中的实现：

          
1
2
3
4
5
6
7
8
          import numpy as np
from sklearn.naive_bayes import GaussianNB
roadFs = np.array([[1, 3], [2, 3], [3, 3], [1, 2], [2, 2], [3, 2], [1, 1], [2, 1], [3, 1]])
roadLs = np.array(['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i'])
clf_car = GaussianNB()
clf_car.fit(roadFs, roadLs)
print(clf_car.predict([[1.2, 1.2], [2.8, 2.8]]))
>>> ['g' 'c']

        

#决策面

机器学习就是将数据根据特征和标签转换为决策面（分类）。

如下图例：

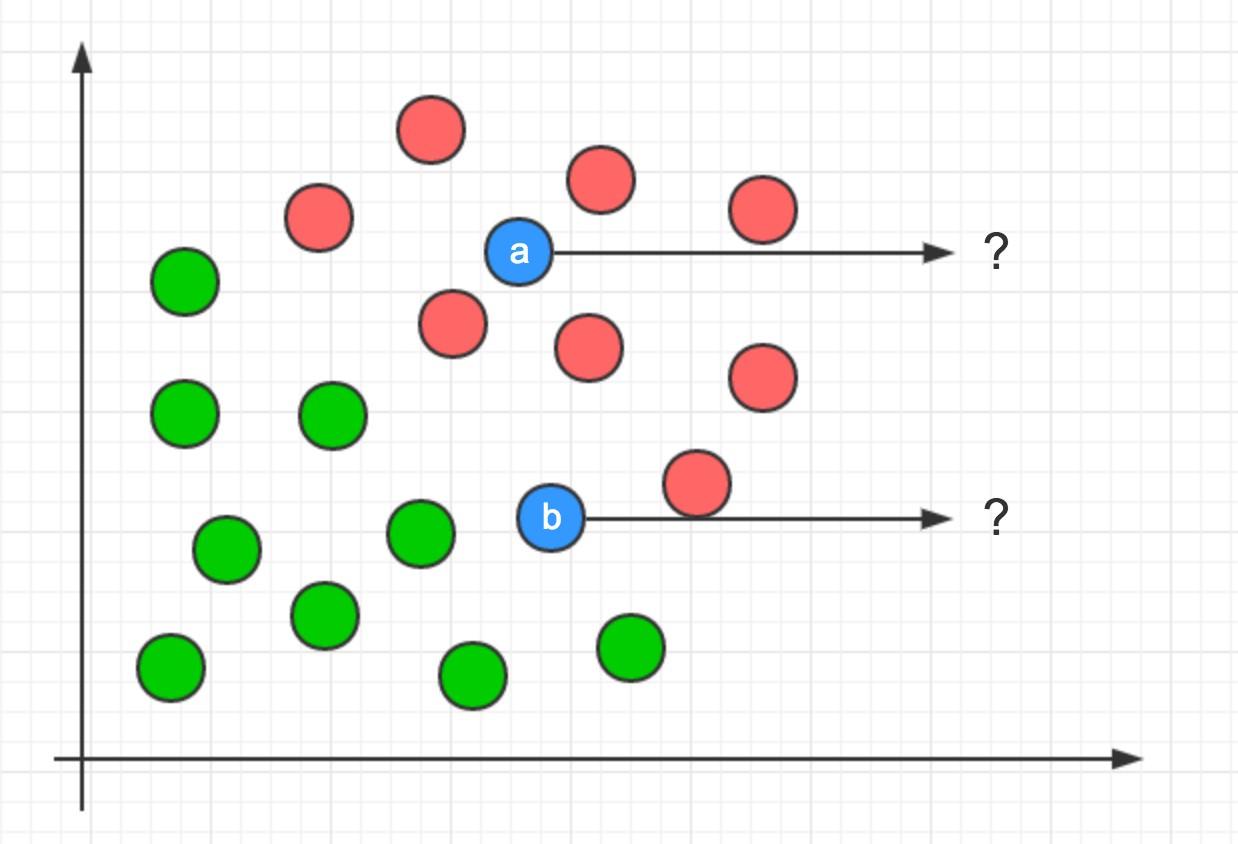
上图中所有数据用圆形标识，我们使用特征将数据分成了两类：红色和绿色，通过直觉判断，数据点a应该被归类于红色数据集，而数据点b显然无法判断。

机器学习能做什么，它可以为以上图例中的数据集决定决策面（分割数据集/分类）。

像这样，它可以计算出一个决策面，决策面左侧即数据绿色数据，右侧反之。

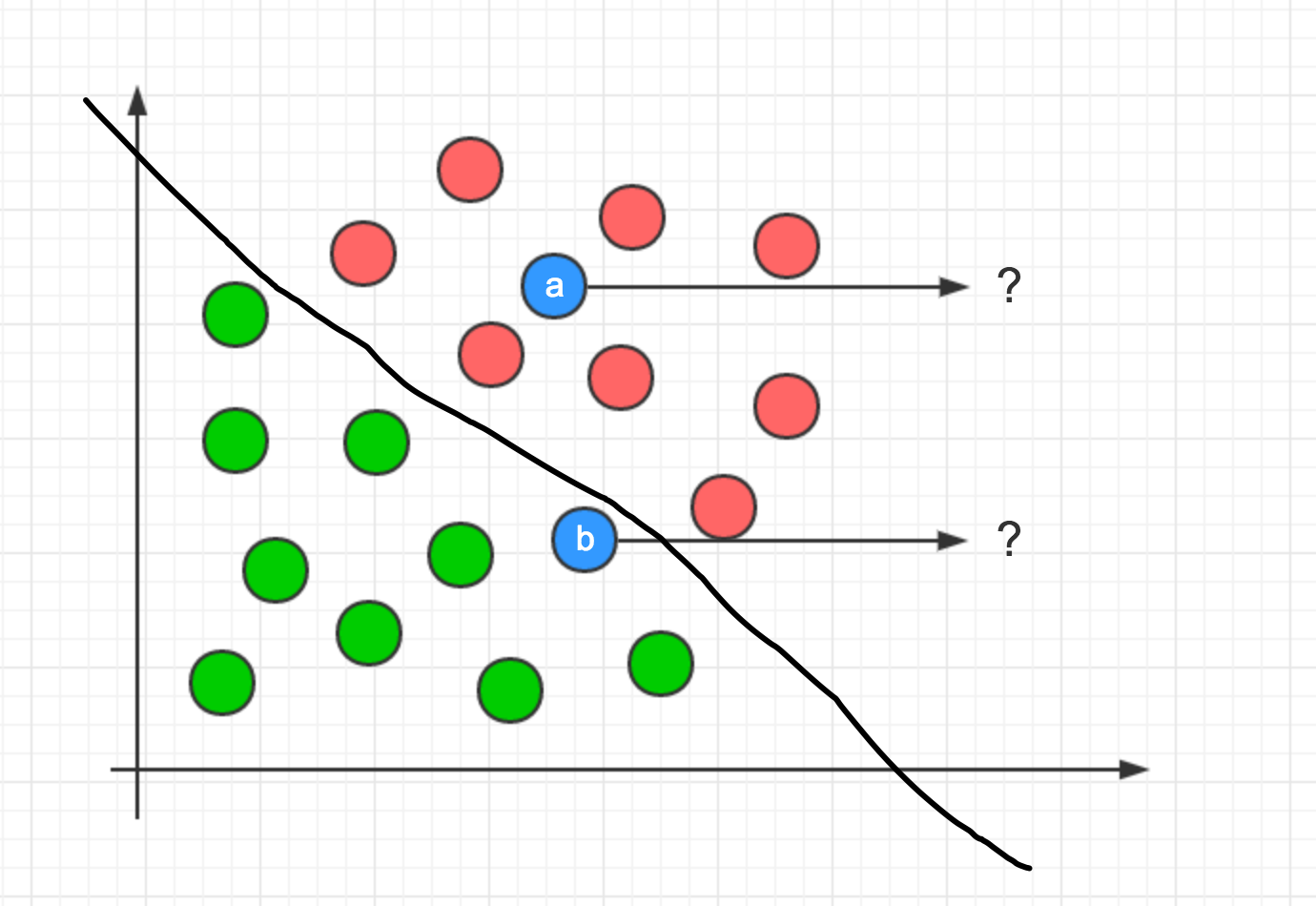
使用决策面，标记数据分类就简单多了。

决策面分为：

• 线层决策面：决策面为一条直线
• 非线性局侧面：决策面不是一条直线（一条直线无法决策的）

#使用算法

常见的计算决策面的算法有：

• 朴素贝叶斯
• 支持向量机
• ...

其之间的不同和详细使用会在之后的文章推出。

基础库： scikit-learn 官网，scikit-learn是一个python学习算法库，包含了丰富的机器学习算法。

完