机器学习算法之朴素贝叶斯

#朴素贝叶斯
在了解朴素贝叶斯之前,我们需要了解一些统计学和概率统计的知识。
Wikipedia 解释:
所谓的贝叶斯方法源于 托马斯·贝叶斯(Thomas Bayes)生前为解决一个“逆概”问题写的一篇文章,而这篇文章是在他死后才由他的一位朋友发表出来的。 在贝叶斯写这篇文章之前,人们已经能够计算“正向概率”,如“假设袋子里面有N个白球,M个黑球,你伸手进去摸一把,摸出黑球的概率是多大”。 而一个自然而然的问题是反过来:“如果我们事先并不知道袋子里面黑白球的比例,而是闭着眼睛摸出一个(或好几个)球,观察这些取出来的球的颜色之后,那么我们可以就此对袋子里面的黑白球的比例作出什么样的推测”。 这个问题,就是所谓的逆概问题。
实际上,贝叶斯当时的论文只是对这个问题的一个直接的求解尝试,并不清楚他当时是不是已经意识到这里面包含着的深刻的思想。 然而后来,贝叶斯方法席卷了概率论,并将应用延伸到各个问题领域,所有需要作出概率预测的地方都可以见到贝叶斯方法的影子,特别地,贝叶斯是机器学习的核心方法之一。 这背后的深刻原因在于,现实世界本身就是不确定的,人类的观察能力是有局限性的(否则有很大一部分科学就没有必要做了——设想我们能够直接观察到电子的运行,还需要对原子模型争吵不休吗?), 我们日常所观察到的只是事物表面上的结果,沿用刚才那个袋子里面取球的比方,我们往往只能知道从里面取出来的球是什么颜色,而并不能直接看到袋子里面实际的情况。 这个时候,我们就需要提供一个猜测(hypothesis,更为严格的说法是“假设”,这里用“猜测”更通俗易懂一点),所谓猜测,当然就是不确定的(很可能有好多种乃至无数种猜测都能满足目前的观测), 但也绝对不是两眼一抹黑瞎蒙——具体地说,我们需要做两件事情:
- 算出各种不同猜测的可能性大小
- 算出最靠谱的猜测是什么
第一个就是计算特定猜测的后验概率,对于连续的猜测空间则是计算猜测的概率密度函数。
第二个则是所谓的模型比较,模型比较如果不考虑先验概率的话就是最大似然方法。
正题:
贝叶斯分类是一系列分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。
在机器学习中,朴素贝叶斯算法(Naive Bayesian) 是其中应用最为广泛的分类算法之一。
朴素贝叶斯是一种常用来计算决策面的算法,它是基于贝叶斯定理与特征条件独立假设的分类方法。
朴素贝叶斯分类器基于一个简单的假定:给定目标值时属性之间相互条件独立。
公式:
P(C|D) = P(D|C) * P(C) / P(D)
公式解读:
P = probability即:可能性、概率C = Category即:分类D = Document即:文档、元素
P(A)即:A发生的可概率P(A|B)即:在B发生的情况下A发生的概率
释义:一个文档属于一个分类的概率 = 当分类出现时,这个文档出现的概率 * 这个分类出现的概率 / 这个文档出现的概率
下面举几个案例,摘自: 阮一峰 - 朴素贝叶斯分类器的应用 :
#病人分类的例子
某个医院早上收了六个门诊病人,如下表。
| 症状 | 职业 | 疾病 |
|---|---|---|
| 打喷嚏 | 护士 | 感冒 |
| 打喷嚏 | 农夫 | 过敏 |
| 头痛 | 建筑工人 | 脑震荡 |
| 头痛 | 建筑工人 | 感冒 |
| 打喷嚏 | 教师 | 感冒 |
| 头痛 | 教师 | 脑震荡 |
现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大?
根据上面的公式我们可以将公式转化为:
P(感冒|打喷嚏x建筑工人) = P(打喷嚏x建筑工人|感冒) x P(感冒) / P(打喷嚏x建筑工人)
释义:一个打喷嚏的建筑工人患上感冒的概率 = 当发生感冒时,打喷嚏的建筑工人的概率 x 感冒者在所有患者中的概率 / 打喷嚏的建筑工人的概率
假定"打喷嚏"和"建筑工人"这两个特征是独立的,即:打喷嚏和你是谁没有关系;因此,上面的等式就变成了:
P(感冒|打喷嚏x建筑工人) = P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒) / P(打喷嚏) x P(建筑工人)
释义:一个打喷嚏的建筑工人患上感冒的概率 = 发生感冒时,打喷嚏者的概率 x 感冒时,建筑工人的概率 x 感冒者在所有患者中的概率 / 打喷嚏者的概率 x 建筑工人的概率
然后就可以计算了:
P(感冒|打喷嚏x建筑工人) = 0.66 x 0.33 x 0.5 / 0.5 x 0.33 = 0.66
因此,这个打喷嚏的建筑工人,有66%的概率是得了感冒。同理,可以计算这个病人患上过敏或脑震荡的概率。比较这几个概率,就可以知道他最可能得什么病。 这就是贝叶斯分类器的基本方法:在统计资料的基础上,依据某些特征,计算各个类别的概率,从而实现分类。
上面例子中:统计资料就是那个表格,特征就是表格中的每项的概率,最终我们将打喷嚏的建筑工人归类为感冒。
#朴素贝叶斯分类器的公式
假设某个体有n项特征(Feature),分别为F1、F2、...、Fn。现有m个类别(Category),分别为C1、C2、...、Cm。贝叶斯分类器就是计算出概率最大的那个分类,也就是求下面这个算式的最大值:
P(C|F1F2...Fn) = P(F1F2...Fn|C) * P(C) / P(F1F2...Fn)
由于 P(F1F2...Fn) 对于所有的类别都是相同的,可以省略,问题就变成了求下面公式的最大值:
P(F1F2...Fn|C) * P(C)
朴素贝叶斯分类器则是更进一步,假设所有特征都彼此独立,因此:
P(F1F2...Fn|C)P(C) = P(F1|C)P(F2|C) ... P(Fn|C)P(C)
上式等号右边的每一项,都可以从统计资料中得到,由此就可以计算出每个类别对应的概率,从而找出最大概率的那个类。 虽然"所有特征彼此独立"这个假设,在现实中不太可能成立,但是它可以大大简化计算,而且有研究表明对分类结果的准确性影响不大。
#账号分类的例子
本例摘自张洋的 #算法杂货铺----分类算法之朴素贝叶斯分类 。
根据某社区网站的抽样统计,该站10000个账号中有89%为真实账号(设为C0),11%为虚假账号(设为C1),先验概率。
C0 = 0.89C1 = 0.11
接下来,就要用统计资料判断一个账号的真实性。假定某一个账号有以下三个特征:
F1: 日志数量/注册天数F2: 好友数量/注册天数F3: 是否使用真实头像(真实头像为1,非真实头像为0)
F1 = 0.1F2 = 0.2F3 = 0
请问该账号是真实账号还是虚假账号? 方法是使用朴素贝叶斯分类器,计算下面这个计算式的值。
P(F1|C)P(F2|C)P(F3|C)P(C)
公式解析:
P(C|F1F2F3) = P(F1F2F3|C) * P(C) / P(F1F2F3)
等同于:
P(C|F1F2F3) = P(F1|C) * P(F2|C) * P(F3|C) * P(C) / P(F1F2F3)
虽然上面这些值可以从统计资料得到,但是这里有一个问题:F1和F2是连续变量,不适宜按照某个特定值计算概率。
一个技巧是将连续值变为离散值,计算区间的概率。比如将F1分解成[0, 0.05]、(0.05, 0.2)、[0.2, +∞]三个区间,然后计算每个区间的概率。
在我们这个例子中,F1等于0.1,落在第二个区间,所以计算的时候,就使用第二个区间的发生概率。
根据统计资料,可得:
P(F1|C0) = 0.5, P(F1|C1) = 0.1P(F2|C0) = 0.7, P(F2|C1) = 0.2P(F3|C0) = 0.2, P(F3|C1) = 0.9
因此:
P(F1|C0) * P(F2|C0) * P(F3|C0) * P(C0) = 0.5 x 0.7 x 0.2 x 0.89 = 0.0623P(F1|C1) * P(F2|C1) * P(F3|C1) * P(C1) = 0.1 x 0.2 x 0.9 x 0.11 = 0.00198
最终得出,后验概率:
P(C0|F1F2F3) = 0.0623 / (0.0623 + 0.00198) = 96.9%P(C1|F1F2F3) = 0.00198 / (0.0623 + 0.00198) = 3.08%
可以看到,虽然这个用户没有使用真实头像,但是他是真实账号的概率,比虚假账号高出30多倍,因此判断这个账号为真。
#在机器学习中的应用
- 学习文档或文本
如下面的例子,看图:
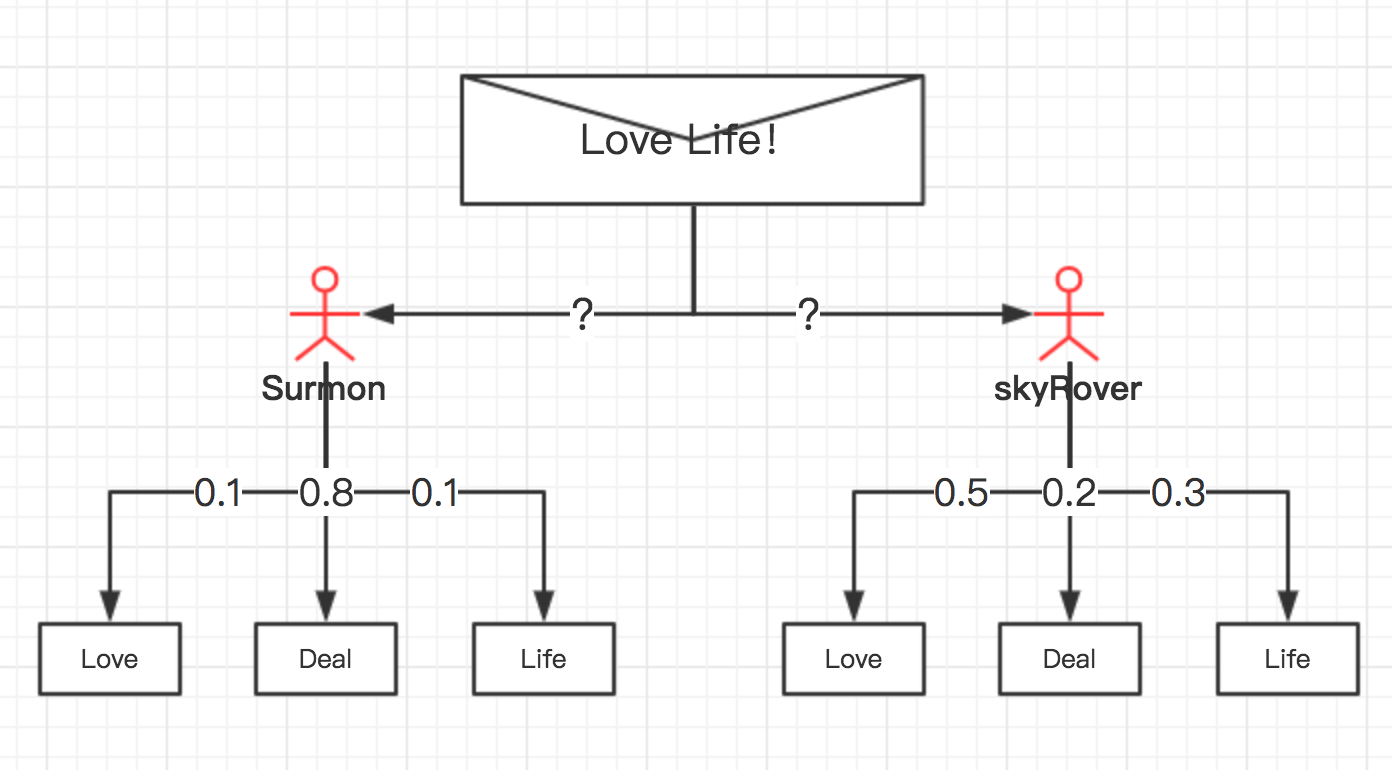
假设有 Surmon 和 Skyrover 两个人,都经常使用电子邮件,为简单区间,我们假设两者发送的所有邮件都只包含3个词语:Love、Deal、Life,两个人的区别在于使用这些词语的频率不同;
Surmon 喜欢谈论Deal,假设他使用Deal词语的概率为80%/0.8,使用Love、Life两个词语的概率均为10%/0.1;
而 Skyrover 则更喜欢谈论Love,较少谈论Deal和Life,假设他使用Love词语的概率为50%/0.5,Deal、Life分别为20%/0.2和30%/0.3;
下面,有这样一封邮件,你认为更有可能是谁发出的?
邮件内容为:Love Life!
在分析之前,我们假设各自发送的概率各占一半,都是50%;
于是,我们可以使用基本形式判断:
P(Surmon) = 0.5(先验概率)P(Skyrover) = 0.5(先验概率)
基本不需要判断,因为,明显邮件中涉及的词语符合 Skyrover 使用词语的频率,所以, Skyrover 发出邮件的概率最大。
然而,又有一封邮件,内容是:Life Deal!
这次邮件又最有可能是谁发出的?
上面我们已经假设两者的先验概率(假设)均为50%,同时:
- Surmon 使用
Life的频率为0.1,使用Deal的频率为0.8; - Skyrover 使用
Life的频率为0.3,使用Deal的频率为0.2;
于是,得到公式:
P(Surmon|'Life Deal') = P('Life'|Surmon) * P('Deal'|Surmon) * P(Surmon) / P('Life Deal')P(Skyrover|'Life Deal') = P('Life'|Skyrover) * P('Deal'|Skyrover) * P(Skyrover) / P('Life Deal')
将先验概率和特征进行计算:
**Surmon: **
P('Life Deal'|Surmon) * P(Surmon)P('Life'|Surmon) * P('Deal'|Surmon) * P(Surmon)0.1 * 0.8 * 0.5 = 0.04
**Skyrover: **
P('Life Deal'|Skyrover) * P(Skyrover)P('Life'|Skyrover) * P('Deal'|Skyrover) * P(Skyrover)0.3 * 0.2 * 0.5 = 0.03
得出后验概率:
P(Surmon|'Life Deal') = 0.04 / (0.04 + 0.03) = 0.57 = 57%P(Skyrover|'Life Deal') = 0.03 / (0.04 + 0.03) = 0.43 = 43%
所以最终,Surmon 发出邮件的概率最高。
#常用模型
#高斯朴素贝叶斯
在实际分类问题中,有些特征可能是连续型变量,比如说人的身高,物体的长度,这些特征可以转换成离散型的值; 比如:如果身高在160cm以下,特征值为1;在160cm和170cm之间,特征值为2;在170cm之上,特征值为3。 也可以这样转换,将身高转换为3个特征,分别是f1、f2、f3,如果身高是160cm以下,这三个特征的值分别是1、0、0,若身高在170cm之上,这三个特征的值分别是0、0、1。
不过这些方式都不够细腻,高斯模型可以解决这个问题。高斯模型假设这些一个特征的所有属于某个类别的观测值符合高斯分布,也就是:
P(xi|yk)=12πσ2yk√exp(−(xi−μyk)22σ2yk)
一个sklearn中的示例:
python
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> iris.feature_names # 四个特征的名字
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
>>> iris.data
array([[ 5.1, 3.5, 1.4, 0.2],
[ 4.9, 3. , 1.4, 0.2],
[ 4.7, 3.2, 1.3, 0.2],
[ 4.6, 3.1, 1.5, 0.2],
[ 5. , 3.6, 1.4, 0.2],
[ 5.4, 3.9, 1.7, 0.4],
[ 4.6, 3.4, 1.4, 0.3],
[ 5. , 3.4, 1.5, 0.2],
......
[ 6.5, 3. , 5.2, 2. ],
[ 6.2, 3.4, 5.4, 2.3],
[ 5.9, 3. , 5.1, 1.8]]) #类型是numpy.array
>>> iris.data.size
600 #共600/4=150个样本
>>> iris.target_names
array(['setosa', 'versicolor', 'virginica'],
dtype='|S10')
>>> iris.target
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,....., 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, ......, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
>>> iris.target.size
150
>>> from sklearn.naive_bayes import GaussianNB
>>> clf = GaussianNB()
>>> clf.fit(iris.data, iris.target)
>>> clf.predict(iris.data[0])
array([0]) # 预测正确
>>> clf.predict(iris.data[149])
array([2]) # 预测正确
>>> data = numpy.array([6,4,6,2])
>>> clf.predict(data)
array([2]) # 预测结果很合理
#多项式朴素贝叶斯
该模型常用于文本分类,特征是单词,值是单词的出现次数。
P(xi|yk)=Nykxi+αNyk+αn
其中:
Nykxi是类别yk下特征xi出现的总次数;Nyk是类别yk下所有特征出现的总次数。
对应到文本分类里,如果单词word在一篇分类为label1的文档中出现了5次,那么Nlabel1,word的值会增加5。
如果是去除了重复单词的,那么Nlabel1,word的值会增加1。n是特征的数量,在文本分类中就是去重后的所有单词的数量。α的取值范围是[0,1],比较常见的是取值为1。
待预测样本中的特征xi在训练时可能没有出现,如果没有出现,则Nykxi值为0,如果直接拿来计算该样本属于某个分类的概率,结果都将是0。在分子中加入α,在分母中加入αn可以解决这个问题。
下面的代码来自sklearn的示例:
python
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
>>> import numpy as np
>>> X = np.random.randint(5, size=(6, 100))
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> from sklearn.naive_bayes import MultinomialNB
>>> clf = MultinomialNB()
>>> clf.fit(X, y)
MultinomialNB(alpha=1.0, class_prior=None, fit_prior=True)
>>> print(clf.predict(X[2]))
多项式模型在训练一个数据集结束后可以继续训练其他数据集而无需将两个数据集放在一起进行训练。
在sklearn中,MultinomialNB()类的partial_fit()方法可以进行这种训练。
这种方式特别适合于训练集大到内存无法一次性放入的情况。
在第一次调用partial_fit()时需要给出所有的分类标号。
python
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
>>> import numpy
>>> from sklearn.naive_bayes import MultinomialNB
>>> clf = MultinomialNB()
>>> clf.partial_fit(numpy.array([1,1]), numpy.array(['aa']), ['aa','bb'])
GaussianNB()
>>> clf.partial_fit(numpy.array([6,1]), numpy.array(['bb']))
GaussianNB()
>>> clf.predict(numpy.array([9,1]))
array(['bb'], dtype='|S2')
#伯努利朴素贝叶斯
伯努利模型中,对于一个样本来说,其特征用的是全局的特征。
在伯努利模型中,每个特征的取值是布尔型的,即true和false,或者1和0。在文本分类中,就是一个特征有没有在一个文档中出现。
如果特征值xi值为1:
P(xi|yk) = P(xi=1|yk)
如果特征值xi值为0:
P(xi|yk) = 1−P(xi=1|yk)
这意味着,“没有某个特征”也是一个特征。
python
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
>>> import numpy as np
>>> X = np.random.randint(2, size=(6, 100))
>>> Y = np.array([1, 2, 3, 4, 4, 5])
>>> from sklearn.naive_bayes import BernoulliNB
>>> clf = BernoulliNB()
>>> clf.fit(X, Y)
BernoulliNB(alpha=1.0, binarize=0.0, class_prior=None, fit_prior=True)
>>> print(clf.predict(X[2]))
sklearn的BernoulliNB()类也有partial_fit()函数。
#多项式模型和伯努利模型在文本分类中的应用
在 #基于naive bayes的文本分类算法 给出了很好的解释。
在多项式模型中:
在多项式模型中, 设某文档d = (t1,t2,…,tk),tk是该文档中出现过的单词,允许重复,则:
先验概率P(c) = 类c下单词总数 / 整个训练样本的单词总数
类条件概率P(tk|c) = (类c下单词tk在各个文档中出现过的次数之和+1) / (类c下单词总数+|V|)
V是训练样本的单词表(即抽取单词,单词出现多次,只算一个),|V|则表示训练样本包含多少种单词。
P(tk|c)可以看作是单词tk在证明d属于类c上提供了多大的证据,而P(c)则可以认为是类别c在整体上占多大比例(有多大可能性)。
在伯努利模型中:
P(c) = 类c下文件总数 / 整个训练样本的文件总数
P(tk|c) = (类c下包含单词tk的文件数+1) / (类c下单词总数+2)
#优劣
#优点
朴素贝叶斯非常易与执行,它的特征空间非常大,在两万单词到二十万之间,运行容易、有效。
#缺点
朴素贝叶斯有间断的缺陷,如在搜索引擎搜索"广州恒大",这是一支球队,但算法会认为是“广州”、“恒大”两个词汇,最终反馈出和这两个词汇有关的事物, 所以由多个单词组成且意义明显不同的短语就不太适合朴素贝叶斯了。
所以不能把监督分类学习当成一个黑盒学习,而是把他们当成一种理论性理解,应关注算法如何运行,以及是否适合你需要解决的问题。
#朴素贝叶斯朴素在哪里
以上面的文本处理例子为例,实际上一段文本交给我们的时候,我们是不知道他应该被归类于哪一个分类的;上面的两个人物 Surmon 和 Skyrover 可以被看做是两个分类,或两个标签; 这两个标签对我们来说实际上是“隐藏的”,我们只能看到这两个标签所表现出来的特征,比如上文中两个人使用词汇的频率便是他们的特征,特征会为我们提供它是谁的证据, 换句话说我们不知道目标元素该归类为谁,但我可以推断目标元素的特征和哪个标签表现的特征最为相似,依此把目标元素归类; 当然,如果两个标签表现的特征一致,那就没法判断了,也不需要判断了; 我们能做的就是根据不同的特征,计算出最大概率,在上文中就是将所有相关的词汇的概率相乘,谁的概率最大,则最终归类为谁。
然而,在上文的文本处理中,我们的算法仅仅关注了词汇的频率特征,我们的乘积仅仅是将词汇频率进行相乘,忽略了词汇的先后顺序; 在自然语言处理中,如果忽略了词汇的先后顺序,文本将变得无意义,所以它并没有真正理解文本,它只能把词汇的频率当成一种分类方法,这就是其“朴素”的原因,但在大多数情况下这已经够用了。
#实践
最终我还是在Javascript上实践了一套伯努利模型的算法, 代码在此 ,已发布 NPM 包,当然也有 Web体验版 。
资料来源:
- sklearn - Naive Bayes
- sklearn - GaussianNB
- sklearn - MultinomialNB
- sklearn - BernoulliNB
- #数学之美番外篇:平凡而又神奇的贝叶斯方法
- #算法杂货铺----分类算法之朴素贝叶斯分类
- 阮一峰 - 朴素贝叶斯分类器的应用
- stick-learn朴素贝叶斯的三个常用模型:高斯、多项式、伯努利
完





看前辈的代码在naivebayes第214行求类条件概率时,实际上实现的是多项式模型,并不是在这边文章中实践一栏所述的实现了伯努利模型。
我觉得你说的很正确!哈哈哈 因为我的数学很渣,写这个库的时候自己也没有弄很清楚; 后来其实还有个 1.0 版本,是要把三种模型都实现,如果你有兴趣的话,完全可以重新实现一个或者 PR 分叉实现后合并一个!